diff --git a/matching.md b/matching.md
index f6c399c..e53a934 100644
--- a/matching.md
+++ b/matching.md
@@ -77,6 +77,22 @@ for (int i = 0; i < n; i++) {
Раскрасим ребра из паросочетания, соответствующего $A$ в красный цвет, $B$ — в синий, а ребра из обоих паросочетаний — в пурпурный. Рассмотрим граф из только красных и синих ребер. Любая компонента связности в нём представляет собой либо путь, либо цикл, состоящий из чередующихся красных и синих ребер. В любом цикле будет равное число красных и синих рёбер, а так как всего синих рёбер больше, то должен существовать путь, начинающийся и оканчивающийся синим ребром — он и будет увеличивающей цепью для $A$, а значит $A$ не оптимальное, и мы получили противоречие.
+## Почему из каждой вершины мы запускаем поиск увеличивающей цепи 1 раз?
+
+**Теорема.** Если из вершины $x$ не существует увеличивающей цепи относительно паросочетания $M$ и паросочетание $M′$ получается из $M$ изменением вдоль увеличивающей цепи, тогда из $x$ не существует увеличивающей цепи в $M′$.
+
+**Доказательство** также от противного.
+
+Допустим в паросочетание внесли изменения вдоль увеличивающей цепи $(y⇝z)$ и из вершины $x$ появилась увеличивающий цепь. Заметим, что эта увеличивающая цепь должна вершинно пересекаться с той цепью, вдоль которой вносились изменения, иначе такая же увеличивающая цепь из $x$ существовала и в исходном паросочетании.
+Пусть $p$ – ближайшая к $x$ вершина, которая принадлежит и новой увеличивающей цепи и цепи $(y⇝z)$.
+
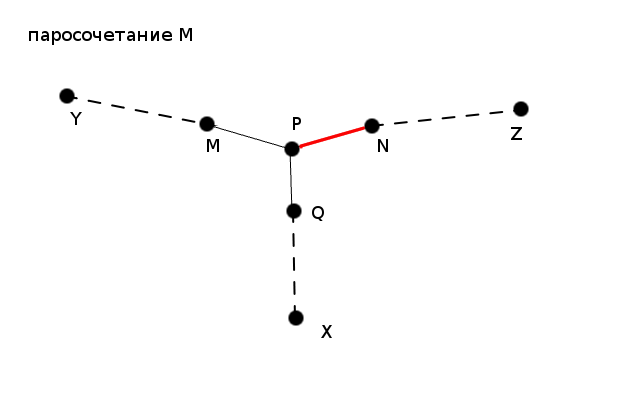
+Тогда $MP$ – последнее ребро на отрезке $(y⇝p)$ цепи $(y⇝z)$, $NP$ – последнее ребро на отрезке $(z⇝p)$ цепи $(y⇝z)$, $QP$ - последнее ребро лежащее на отрезке $(x⇝p)$ новой увеличивающей цепи. Допустим $MP$ принадлежит паросочетанию $M′$, тогда $NP$ ему не принадлежит. (Случай, когда $NP$ принадлежит паросочетанию $M′$ полностью симметричен.)
+
+
+
+
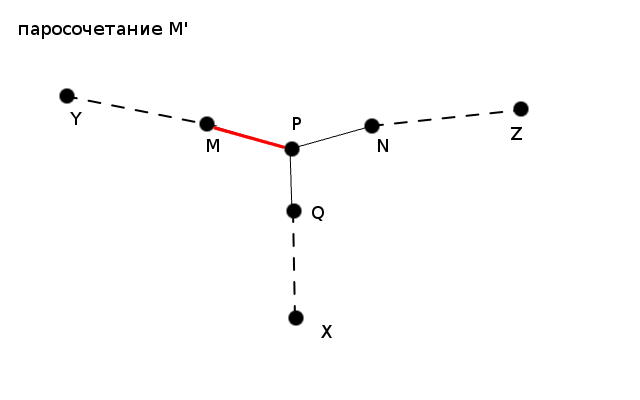+Поскольку паросочетание $M′$ получается из $M$ изменением вдоль увеличивающей цепи $(y⇝z)$, в паросочетание $M$ входило ребро $NP$, а ребро $MP$ нет. Кроме того, ребро $QP$ не лежит ни в исходном паросочетании $M$, ни в паросочетании $M′$, в противном случае оказалось бы, что вершина $p$ инцидентна нескольким рёбрам из паросочетания, что противоречит определению паросочетания. Тогда заметим, что цепь $(x⇝z)$, полученная объединением цепей $(x⇝p)$ и $(p⇝z)$, по определению будет увеличивающей в паросочетании $M$, что приводит к противоречию, поскольку в паросочетании $M$ из вершины $x$ не существует увеличивающей цепи.
+
## Скорость работы
Такой алгоритм ровно $n$ раз ищет увеличивающий путь, каждый раз просматривая не более $m$ рёбер, а значит работает за $O(nm)$.