1857. Largest Color Value in a Directed Graph #1730
-
|
Topics: There is a directed graph of You are given a string A valid path in the graph is a sequence of nodes Return the largest color value of any valid path in the given graph, or Example 1:
Example 2:
Constraints:
Hint:
|
Beta Was this translation helpful? Give feedback.
Replies: 1 comment 2 replies
-
|
We need to determine the largest color value in a directed graph, considering possible cycles. If the graph contains a cycle, we return -1. Otherwise, we compute the maximum color value using dynamic programming combined with topological sorting. Approach
Let's implement this solution in PHP: 1857. Largest Color Value in a Directed Graph <?php
/**
* @param String $colors
* @param Integer[][] $edges
* @return Integer
*/
function largestPathValue($colors, $edges) {
$n = strlen($colors);
$m = count($edges);
$reverse_adj = array_fill(0, $n, array());
$original_adj = array_fill(0, $n, array());
$in_degree = array_fill(0, $n, 0);
foreach ($edges as $edge) {
$a = $edge[0];
$b = $edge[1];
$original_adj[$a][] = $b;
$reverse_adj[$b][] = $a;
$in_degree[$b]++;
}
$queue = new SplQueue();
$top_order = array();
for ($i = 0; $i < $n; $i++) {
if ($in_degree[$i] == 0) {
$queue->enqueue($i);
}
}
while (!$queue->isEmpty()) {
$u = $queue->dequeue();
$top_order[] = $u;
foreach ($original_adj[$u] as $v) {
$in_degree[$v]--;
if ($in_degree[$v] == 0) {
$queue->enqueue($v);
}
}
}
if (count($top_order) != $n) {
return -1;
}
$dp = array();
$max_color = 0;
foreach ($top_order as $u) {
$color = $colors[$u];
$color_index = ord($color) - ord('a');
$current_dp = array_fill(0, 26, 0);
$current_dp[$color_index] = 1;
foreach ($reverse_adj[$u] as $v) {
for ($c = 0; $c < 26; $c++) {
$temp = $dp[$v][$c] + ($color_index == $c ? 1 : 0);
if ($temp > $current_dp[$c]) {
$current_dp[$c] = $temp;
}
}
}
$current_max = max($current_dp);
if ($current_max > $max_color) {
$max_color = $current_max;
}
$dp[$u] = $current_dp;
}
return $max_color;
}
$colors = "abaca";
$edges = [[0,1],[0,2],[2,3],[3,4]];
echo largestPathValue($colors, $edges); // Output: 3
$colors = "a";
$edges = [[0,0]];
echo largestPathValue($colors, $edges); // Output: -1
?>Explanation:
This approach efficiently combines topological sorting and dynamic programming to solve the problem in linear time relative to the number of edges and nodes, making it suitable for large input sizes. |
Beta Was this translation helpful? Give feedback.
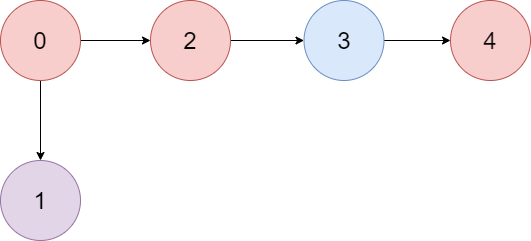
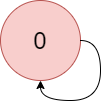
We need to determine the largest color value in a directed graph, considering possible cycles. If the graph contains a cycle, we return -1. Otherwise, we compute the maximum color value using dynamic programming combined with topological sorting.
Approach
dp[u][c]represents the maximum count of colorcin any path ending at nodeu.